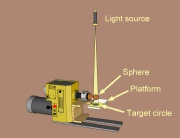
Sphere – Shadow Method
This is the easiest and most direct method for turning a sphere, in my opinion. No marking on the blank nor rechucking between cup centers is required. You get instant feedback as you turn the blank from a cylinder to a sphere.
The idea is to use a small spotlight mounted above the lathe to cast a shadow of the blank onto a target circle located underneath it. To turn the sphere, simply remove wood until the shadow of the blank fits inside the target circle.
Some preparation is required. An appropriate source of light must be provided and you must build a platform to hold the target circle. However, neither the platform nor the light source require working to close tolerances.
Credit for this method goes to David Reed Smith. Links to his website and an explanation of the process are given at the end of this article.
The Light Source
A sharper shadow will be produced if the light source is located as high as possible above the lathe. Further, the source should have a small diameter and should project a beam of light so you get the most illumination where it’s needed.
I’ve tried two different sources. One is a 35 watt halogen flood lamp mounted about
40” above the spindle of my lathe. The other is a small 3-
The mount for the halogen lamp is a crude affair that snaps into the metal grid of the drop ceiling above my lathe. A porcelain socket holds the bulb, and a small frame underneath the bulb holds the baffle.
Note: A halogen lamp gets really hot. If you use one, do not use cardboard for the baffle; it will catch fire in short order. I used thin aluminum, the kind used for flashing when you install a roof. Also, the construction is open so that air can circulate freely around the bulb and socket. There is no reason to enclose the bulb.
My LED flashlight simply hangs by a wire from the baffle made for the halogen bulb. The wire is attached to the flashlight by way of a small end cap that gives a friction fit against the rubbery surface of the flashlight.
Another end cap with a 1/2” hole fits over the business end of the flashlight to limit the diameter of the light source. It too is held on by friction.
The light source should be directly above the center of the sphere. A plumb bob is handy for positioning the source but not essential. Absolute precision is not required.
Which source do I use? Even though both work well, I use the halogen bulb to avoid having to deal with batteries for the flashlight.
I’ve found that I need some ambient light in the room in order to see the target circle. I turn off the lights directly above my lathe but leave the lights on in the more distant parts of the shop.
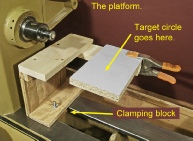
The Platform
My platform is supported at only one end so the banjo can slide underneath it. It
has a U-
The top surface is about 3” below the centerline of the spindle. This will accommodate a sphere approaching 6” in diameter, a rather large sphere.
Splitting Hairs
Strictly speaking, the diameter of the sphere and that of its shadow will not be the same; the shadow will be slightly larger. This is because the light rays diverge as they travel from the source.
For a typical setup, the diameter of the shadow will be about 10% larger than that of the sphere. If that difference is not important to your work, you may skip this section. Otherwise, press on.
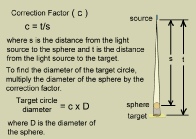
A correction factor ( c ) can be calculated for your system based on the distance the light source is above the spindle and how far below the spindle the top surface of the platform and target circle is:
Correction factor = distance source to spindle / distance source to target
c = t / s
where t is the distance from the source to the platform and s is the distance from the source to the center of the spindle.
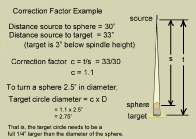
For my halogen system, the source is 40” above the spindle. It is 43” above the target circle because my platform is 3” below the center of the spindle. Therefore, the correction factor is
c = t / s = 43” / 40”
c = 1.075
Now suppose we want to turn a sphere as close to 2.90” in diameter as we can because this is the diameter of a baseball. How large should the target circle be?
Target circle diameter = correction factor x diameter of the sphere
= c x D
= 1.075 x 2.90” = 3.118”
If we turn a baseball without applying the correction, the ball will turn out about 7/32” undersize. Is this important? Maybe, or maybe not.
Once you calculate the correction factor, it will not change as long as you do not change the height of your light source nor the height of your platform. So, calculate it once and write it on the wall.
Here’s something that won’t work. Suppose you have a cylindrical blank for a sphere
mounted on your lathe, already trued up and ready to roll. You cannot simply measure
the diameter of the blank and make the target circle the same size. If you do, you
will wind up making your sphere smaller than what it could have been. Bite the bullet
and apply the correction factor to find how much larger the target needs to be. That
way you will get the biggest sphere possible.
sphere
mounted on your lathe, already trued up and ready to roll. You cannot simply measure
the diameter of the blank and make the target circle the same size. If you do, you
will wind up making your sphere smaller than what it could have been. Bite the bullet
and apply the correction factor to find how much larger the target needs to be. That
way you will get the biggest sphere possible.
Here’s something that works pretty well. If you have a trued- lathe
and want to make a target circle for it, measure the width of the shadow cast by
the blank and use that as the diameter of the target circle. This avoids having to
use the correction factor. Measuring a shadow involves a bit of judgement (It’s hard
to get a grip on a shadow.) but the results can be good.
lathe
and want to make a target circle for it, measure the width of the shadow cast by
the blank and use that as the diameter of the target circle. This avoids having to
use the correction factor. Measuring a shadow involves a bit of judgement (It’s hard
to get a grip on a shadow.) but the results can be good.
Turn a Sphere!
My suggestion is to begin with a sphere about 2.5 to 3” in diameter. Find a blank
about 5” long, put it between centers, and form a tenon on one end. Mount the blank
in a scroll chuck and bring up the tailstock for support. 
True up the blank and turn it to a uniform cylinder. Measure its diameter. This will be the largest sphere you can get from that blank, but you will get it only if you make the target circle a bit larger by applying the correction factor as described above.
On an index card or other piece of card stock, draw the target circle. Carefully center the circle in the shadow of the cylinder and tape the card to the top of the platform. Locate the circle a short distance back from the end of the blank to avoid having the dimple made by the point of the live center appear on the surface of your sphere.
Position the tool rest so you can see past it to the target circle. If the cutting
tool is applied to the blank at center height, you will be able to see the shadow
of the tip of the tool while you are cutting.
target circle. If the cutting
tool is applied to the blank at center height, you will be able to see the shadow
of the tip of the tool while you are cutting.
Some practice may be required for you to become accustomed to the cutting process. This is quite similar to being able to make a cut while looking across the top (horizon) of a workpiece instead of looking where the tool makes contact with the wood. In this case you will be looking at the shadow cast on the target circle.
The next photos show further progress and a profile view of the sphere corresponding to the view of the shadow.
As you near completion of the sphere, do the sanding before reducing the diameter of the nubbin significantly.
Finally, turn the nubbin down as small as you dare, then use a parting tool, long point of a skew, or a small saw to separate the sphere from the rest of the blank.
Removing the Nubbin and Sanding its Footprint
Exercise caution when removing the nubbin to avoid having it break off and pull fibers out of the surface of the sphere. When in doubt, cut it long and sand it away.
My preference is to mount a soft sanding pad in a Beall collet chuck mounted on my lathe. (Photo in previous article.) I begin with 180 grit if I have considerable material to remove. This is often the case because I typically, for some reason, leave a bump at the foot of the nubbin.
Once I get the footprint sanded down close to the final surface, I switch to a higher
grit, typically 220, and continue. With the lathe running fairly slowly, I keep the
sphere moving in a more-
If you use a soft pad with the lathe turning slowly, the sandpaper will conform to the surface of the sphere and make it less likely that you will create a flat spot if you happen to linger a bit too long in one area.
After the sanding, all that remains is to apply the finish of your choice and the sphere will be done.
Sanding during the Finishing Process
Sometimes it seems that just as soon as you remove a sphere from the lathe, you wish
you could put it back on, briefly, to touch up a spot that needs a bit more sanding.
Or, if you embark on a finishing process that involves multiple layers of finish with sanding in between, it is convenient to be able to stick it back on the lathe.
with sanding in between, it is convenient to be able to stick it back on the lathe.
This can be done with cup centers but they are a bit cumbersome to use. On the other hand, a small vacuum chuck is ideal. You basically stick the sphere on the chuck, turn on the lathe, and sand away. Further, changing the axis of rotation is quick and easy.
A link is given below to an article on this site that shows how to make a vacuum chuck for the specific purpose of holding spheres for sanding.
Credits and Links
David Reed Smith
https://www.youtube.com/watch?v=1oMMIoARLt4
http://www.davidreedsmith.com/Articles/ShadowSphereJig/ShadowS phereJig.htm